Faisabilité & Equilibre
Comme nous l'avons déjà rappelé, l'équation bilan ne préjuge pas de la tangibilité d'une réaction chimique. De surcroît, il faut garder présent à l'esprit que, même pour une réaction dont la faisabilité expérimentale s'est avérée, la transformation chimique évolue simultanément dans deux directions :
celle recherchée selon l'équation bilan réactifs → produit et celle du sens inverse. En effet, à l'échelle microscopique, les produits peuvent, à leur tour, se transformer spontanément en réactifs. Selon le deuxième principe, le sens macroscopiquement observé de l'évolution du système correspond à celui pour lequel la variation d'énergie libre est négative. Toutefois, quel que soit le sens prédominant de l'évolution, l'avancement de la réaction est limité à la position de l'équilibre. Celle-ci est atteint lorsque, par unité de temps, le nombre de molécules "produits" créées est égal au nombre de molécules "produits" qui se consomment. Le système devient alors stationnaire et atteint un équilibre dynamique : ses propriétés macroscopiques n'évoluent plus.
Ainsi, une transformation chimique s'effectue de manière spontanée si, et seulement si, son évolution s'accompagne d'une diminution de l'enthalpie libre de la réaction, GR. Il est donc important de connaître l'expression de la variation de cette grandeur avec l'évolution recherchée du système.
Considérons une réaction à stoechiométrie simple mettant en jeu n espèces moléculaires Aj :
« Σνj.Aj = 0 » (1-2)
Par définition, l'énergie libre de cette réaction, GR, s'écrit :
où Gj représente l'enthalpie libre du corps Aj dans les conditions de la réaction. Cette grandeur est une fonction multi variable dépendant notamment de la température, de la pression et de la composition du système. Dans les conditions isotherme et isobare l'on peut prend, comme seule variable indépendante, la composition du système :
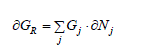
ou, compte tenu de la définition de l'avancement de la réaction (Eq.1-6) :
ou encore :
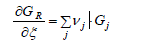
Nous savons, d'autre part, que l'enthalpie libre de chacun des corps Aj peut s'exprimer en fonction de son énergie libre standard Gj° et de son activité aj :
Rappelons que aj est l'activité du corps Aj dans l'état d'avancement de la réaction. L'indice supérieur ° est employé pour désigner l'état standard.
La variation de l'enthalpie libre du système peut alors être obtenue en combinant les deux équations (2-4) et (2-5) :
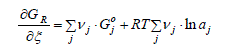
Le premier terme à droite de cette expression est, par définition, égale à la variation d'enthalpie libre standard de réaction, ΔG°R , d'où :
Cette expression décrit la variation de l'enthalpie libre de la réaction dans des conditions quelconques de composition, hors ou à l'équilibre. La fraction représentée par le terme
Πj ajvj est appelée "monôme des activités", M, ou encore le quotient de réaction1 :
1. Le symbole Π est un opérateur mathématique relatif au produit des membres qu'il contient.
A l'équilibre, l'énergie libre GR est minimum autrement dit sa variation est nulle :
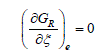
L'indice e se réfère aux conditions d'équilibre. En appliquant la condition d'équilibre à l'équation (2-7), on obtient :
Traditionnellement, le monôme des activités à l'équilibre est baptisé la constante d'équilibre de la réaction :
Ka,e est la constante d'équilibre relative aux activités2. En combinant les deux équations précédentes, nous obtenons :
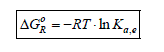
2. Il ne faut pas confondre la constante d'équilibre Ka,e avec le monôme des activités M. En effet, Ka,e. est une valeur particulière de M où figurent les valeurs des activités à l'équilibre thermodynamique.
Comme nous le verrons plus loin, il existe d'autres constantes d'équilibre relatives à d'autres propriétés comme la concentration ou la pression par exemple. Ces constantes ont toutes pour le point commun d'être issues de Ka,e et de se présenter par conséquent par des expressions analogues à celle de l'équation (2-11). A ce titre, on peut citer par exemple :
-
la constante d'équilibre liée aux concentrations « KC,e = Πj Cj,evj »
-
la constante d'équilibre liée aux pressions « Kp,e = Πj pj,evj »
-
la constante d'équilibre liée aux titres molaires « Ky,e = Πj yj,evj et Kx,e = Πj xj,evj »
Cependant, il faut garder présent à l'esprit que seule Ka,e possède un caractère à usage universel et doit être employée dans l'équation(2-12) . Les autres constantes ne sont valables que pour des cas de figure spécifiques (gaz parfait, solution idéale, etc.). Leur usage est donc strictement réservé au cas spécial correspondant et doit être fait avec précaution.
L'expression (2-11) est plus communément connue sous le nom de la loi d'action des masses. Toutefois cette locution est quelque peu malencontreuse dans la mesure où ce ne sont pas les masses mais les activités qui interviennent dans la constante d'équilibre Ka,e. En réalité, cette appellation est maintenue en raison de l'assimilation du système réactionnel à une balance. Si l'on ajoute une masse sur un des plateaux d'une balance en équilibre, il faut ajouter une masse égale sur l'autre plateau pour retrouver l'équilibre. De la même manière, dans un système en équilibre si l'on augmente l'activité d'un ou de plusieurs composants (en modifiant sa composition par exemple) le système se déplace pour trouver à nouveau l'équilibre.
Sens d'évolution d'une réaction chimique
Par définition, dans un système réactionnel hors équilibre, les composants actifs Aj ne sont pas à la même activité. Par conséquent, une évolution macroscopiquement perceptible du système peut avoir lieu (sous réserve de lui fournir l'énergie d'activation). Le sens net de cette évolution (qui peut être conforme ou opposé à celui décrit par la relation stoechiométrique de la réaction) sera, en tout état de cause, celui conduisant à une diminution de l'enthalpie libre du système :
En tenant compte de l'équation (2-7) cette condition implique :
Ou, compte tenu de l'équation (2-12) :
La relation 2-15 permet de connaître le sens d'évolution d'une réaction chimique en comparant la valeur ponctuelle du monôme des activités pour les conditions opératoires, M, à celle de la constante d'équilibre Ka,e. (autrement dit à la valeur que M prend à l'équilibre). La réaction n'évolue dans le sens voulu (désigné par l'équation stoechiométrique) que si M est inférieure à Ka,e. Dans le cas contraire, le système ne peut évoluer que dans le sens inverse. Dans tous les cas, l'évolution tend à réaliser les proportions d'équilibre (M=Ka,e).
Calcul de la composition à l'équilibre d'un système réactionnel
L'équation (2-12) décrit la relation entre les grandeurs thermodynamiques relatives à la réaction et les activités de divers constituants à l'équilibre. Notons que la variation d'enthalpie libre (ΔG°R) ne dépend que de la température et du choix des états standard des constituants actifs. Si sa valeur n'est pas directement accessible, elle peut être déterminée à partir des enthalpies libres de formation (ΔG°f) des constituants actifs de la réaction, disponibles dans les tables thermodynamiques. La difficulté principale lors de l'application de cette équation est donc l'estimation de l'activité des différents composants. En effet, l'activité est une notion très abstraite et difficile à assimiler et encore plus à mesurer. Il convient donc d'exprimer cette grandeur en terme d'autres paramètres plus familiers au lecteur. De plus, sa valeur ne dépend pas uniquement de la nature du composant mais aussi des conditions opératoires et de la nature du milieu réactionnel (gazeux, liquide, etc.). Nous allons présenter ici, l'application de l'équation (2-12) aux cas des réactions chimiques réalisées en milieux homogènes gazeux ou liquide.
-
Réaction homogène en phase gazeuse:
Pour un constituant Aj d'un mélange gazeux, l'activité est définie par le rapport :
où fj est la fugacité du constituant dans le mélange gazeux (exprimé en atm.) et fj° la fugacité de ce même constituant dans un état de référence auquel se réfère l'indice °. Si l'on pose pour fugacité de référence fj°=1 atm. on a :
Le terme numériquement est là pour nous rappeler que aj et fj ont des dimensions différentes. D'une manière générale, la fugacité d'un composant peut être exprimée par sa pression partielle pj et son coefficient de fugacité φ j :
De plus, si la phase gazeuse peut être considéré comme un mélange de gaz parfait (ce qui est une hypothèse raisonnable pour les systèmes à faibles pression (<20 bars)) φ j vaut 1, d'où :
Réaction homogène en phase liquide:
Pour un mélange réactionnel en phase liquide, l'activité d'un composant Aj peut s'exprimer en terme de sa fugacité, de son titre molaire xj dans le mélange et de son coefficient d'activité, γ j :
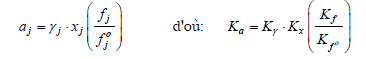
Pour des pressions faibles à modérées, la variation de fugacité entre la pression de référence et celle du système est négligeable (fj°=fj). De plus, si le mélange liquide peut être considéré comme idéal le coefficient d'activité est égal à l'unité. Dans ces conditions on a aj=xj, d'où :
« Ka = Kx » (2-23)
Influence de la pression sur la composition à l'équilibre d'une réaction
Pour un liquide idéal sous une pression faible à modérée, la pression n'influence ni la faisabilité ni l'équilibre de la réaction En revanche, pour un gaz, la fugacité, et par conséquent l'activité, dépend sensiblement de la pression :
« fj = ϕj . pj = ϕj . yj . P et donc Ka = Kϕ . Ky . pΣvj » (2-24)
Signalons que P doit être exprimée en même unité que la fugacité de référence, fj°. Cette équation très importante décrit l'influence de la pression et de la présence d'inertes sur la composition à l'équilibre d'un système réactionnel gazeux.
Influence de la température sur la composition à l'équilibre d'une réaction
Quelle que soit la phase réactionnelle homogène (gaz ou liquide) l'influence de la température est donné par la règle de van't Hoff :
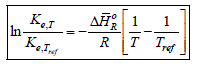
ou :
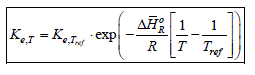
Cette relation permet de calculer la constante d'équilibre d'une réaction chimique à une température T, lorsque l'on connaît l'enthalpie moyenne de la réaction et un couple de valeurs de référence, Kae,Tref et Tref. L'équation (2-25) indique que la constante d'équilibre subie une variation exponentielle négative avec l'inverse de la température. Cette variation est croissante si la réaction est endothermique ( ΔHR > 0 ) et décroissante si elle est exothermique ( ΔHR < 0 ), comme le montre la figure 1.

Principe de Le Chatelier
Il est intéressant de constater que les différents sujets passés en revu jusqu'ici, traitant de l'influence des différents paramètres d'état sur l'équilibre d'un système réactionnel peuvent être déduits, de manière qualitative, du principe de Le Chatelier. Ce Principe, qui n'est autre que l'extension de la loi d'action de masse aux paramètres d'état autres que la composition, s'énonce :
"Un système en équilibre soumis à une variation d'une de ses variables d'état réagit de manière à réduire ou à annuler cette modification".
Pour un système réactionnel, les paramètres d'état les plus importants sont la température, la pression et la composition du système.
-
Influence de la pression :
Une augmentation de la pression amène le système à évoluer dans la direction qui conduit à réduire la pression et vice versa.
-
Influence de la température :
Une augmentation de la température amène le système à évoluer dans la direction qui absorbera la chaleur c'est à dire dans le sens endothermique et vice versa.
-
Influence de la composition :
Une augmentation de la quantité (ou la concentration) d'une ou plusieurs réactifs amène le système à évoluer dans la direction qui consommera les réactifs et vice versa. De même, une élimination d'un ou plusieurs produits (par évaporation, adsorption ou neutralisation, par exemple) conduit au déplacement du système dans le sens de production de ce(s) constituant(s).
