Approche moléculaire de la cinétique chimique
La loi d'Arrhenius et la règle de vant Hoff, présentées dans le chapitre précédent, ainsi que la loi de vitesse présentées par l'équation (3-5) sont des règles purement empiriques, basées sur une vision globale des processus mis en oeuvre, issue de nombreuses expérimentations. Elles sont, par conséquent, indépendantes de toute hypothèse quant à la nature microscopique des phénomènes mise en jeu. Toutefois, une réaction chimique est un processus complexe se déroulant à l'échelle des molécules. L'objectif de cette partie est d'exposer une approche moléculaire qui permet de réconforter, à partir des fondements théoriques, ces règles empiriques. Cette approche repose sur la théorie cinétique des gaz qui adopte un point de vue statistique qui nécessite de prendre en compte uniquement des valeurs moyenne. On considère que les effets observables (apparition et disparition des moles) sont la résultante des comportements individuels d'un grand nombre de molécules.
Théorie des collisions
Intéressons-nous au cas particulier simple d'une réaction élémentaire bimoléculaire se déroulant en phase gazeuse, comme, par exemple, celle de décomposition de l'iodure d'hydrogène :
« 2 HI → H2 + I2 »
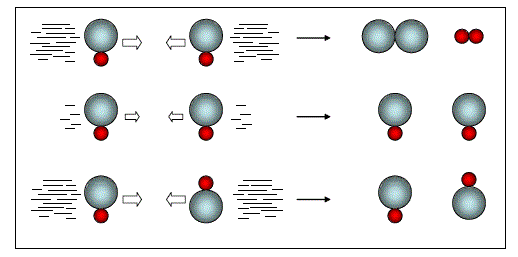
Il est évident que cette transformation ne peut avoir lieu, à la seule condition minimale que deux molécules de réactif se rencontrent. Cette exigence préalable n'est toutefois qu'une condition nécessaire mais pas suffisante pour que la transformation se produise. En effet, pour qu'une collision entre deux molécules de HI s'avère efficace, autrement dit pour qu'elle conduise à la formation des produits (fig. 1), il faut :
-
d'une part, que les deux molécules possèdent une énergie cinétique suffisante pour sinon briser tout au moins modifier les liaisons atomiques existantes,
-
et, d'autre part, que la collision se fasse selon des orientations favorables. Dans le cas considéré ici, il faut que la collision des atomes de HI se fasse sur leur bonne extrêmité.
A l'opposé, si l'énergie de la collision est insuffisante ou que les molécules ne s'orientent pas favorablement la réaction est avortée (figure 1).
Par conséquent, pour une réaction type A + B → produits, la cadence de progression de la réaction sera fonction de :
-
nombre total de collision entre molécules A et B par unité de temps et par unité de volume, appelé " fréquence spécifique de collision", ZAB.
-
fraction des collisions possédant l'énergie requise, appelée "facteur énergétique" désigné par P1,
-
"facteur stérique", P2, défini par fraction des collisions pour lesquelles l'orientation des molécules est favorable.
Les deux derniers facteurs, énergétique et stérique, permettent de déterminer la fraction globale de chocs réussis, P*:
« P* = P1 ⋅ P2 »
Le lecteur peut facilement se convaincre que le nombre de molécules produites par unité de volume et de temps, ^r , est égal au produit de la fréquence des collisions entre les molécules et la fraction globale de chocs réussis :
Voyons maintenant, comment dans le cas d'un milieu homogène en phase gazeuse, la théorie des collisions moléculaires permettra de déterminer certains de ces composants. Cette théorie repose sur une vision très simplifiée des milieux gazeux, largement inspirée de la théorie cinétique des gaz. Dans cette approche, les molécules sont assimilées à des sphères rigides impénétrables en mouvement qui subissent des collisions entre elles. Cependant, seules les collisions binaires sont prises en compte dans ce modèle. De plus, les chocs sont supposés élastiques, sous-entendu qu'au cours d'une collision, la quantité de mouvement et l'énergie cinétique de l'ensemble des deux molécules se conservent. Entre deux collisions successives, chaque molécule se déplace selon une trajectoire rectiligne dont la direction est aléatoire.
Fréquence de collisions, ZAB
Considérons un volume de contrôle V contenant un gaz composé initialement de molécules de A et de B. La concentration des constituants, exprimée en nombre de molécules par unité de volume, s'écrit :
Fixons notre regard, l'espace d'un temps très court, Δt, sur une molécule de A se déplaçant à vitesse relative moyenne constante, υ .
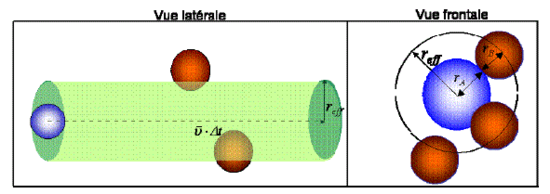
Comme le montre la figure 2, au cours de son déplacement, celle-ci ne peut toucher une molécule de B que si la distance séparant le centre des deux molécules est inférieure à la somme de leur rayon respectif (rA+rB). Par conséquent, nous pouvons définir une "section efficace" notée σ, comme l'aire d'un cercle imaginaire, normal à la direction du mouvement, ayant pour l'épicentre celui de la molécule de A et pour rayon reff=(rA+rB).
La molécule de A se déplaçant dans une direction quelconque va donc balayer un volume efficace défini par celui d'un cylindre ayant une hauteur υ Δt et une base d'aire σ. De toute évidence, elle rentrera en collision avec toute autre molécule dont le centre se trouve à l'intérieur de ce cylindre (figure 2).
Le nombre moyen de collision d'une molécule de A avec ses voisines B, pendant le laps de temps Δt et dans le volume considéré correspond donc au nombre des molécules de B présentes dans le volume efficace. En considérant que les molécules sont réparties de manière homogène dans le volume, ce nombre est :
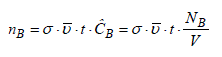
Par conséquent, le nombre total de collision entre toutes les molécules de A avec celles de B est :
et la fréquence spécifique des collisions, autrement dit le nombre total de collisions par unité de temps et par unité de volume :
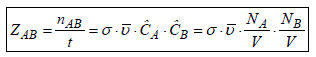
En outre, la théorie cinétique des gaz permet de relier la vitesse relative moyenne des molécules à leur masse et à la température du milieu par la relation :
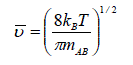
où kB est la constante de Boltzmann et mAB = (m A.mB ) / (mA + mB ) est la masse réduite des molécules. Cependant, les masses molaires, MA et MB, sont souvent plus appropriées que les masses moléculaires pour les calculs :
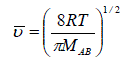
avec R la constante des gaz parfaits et MAB = (MA.MB ) / (MA + MB )
A la lumière des éléments présentés dans ce paragraphe, nous pouvons déduire que la concentration et la température sont les paramètres principaux qui affectent la fréquence des collisions. Une augmentation des concentrations favorise la probabilité des rencontres et la montée de la température fait croître la vitesse moyenne des molécules et donc le nombre de chocs par unité de temps.
Facteur énergétique, P1 :
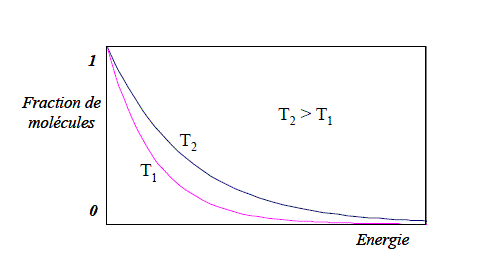
Nous avons postulé dans le paragraphe ? que seules les collisions mettant en jeu une énergie supérieure à une valeur critique pouvaient être efficaces. Ainsi, nous pouvons définir l'énergie d'activation d'une collision, ea, comme l'énergie minimale nécessaire pour provoquer la réaction lors de choc entre deux molécules orientées convenablement. Par ailleurs, la théorie Maxwell du gaz parfait nous indique que, dans un gaz en équilibre isotherme à la température T, la probabilité pour qu'une molécule ait une énergie supérieure à un niveau quelconque e est donnée par le facteur de Boltzmann : exp(-e/kBT) (ou alors exp(-E /RT) si E est l'énergie d'une mole de molécules). A titre indicatif, la figure 3 représente, pour deux températures différentes, la répartition cumulée des fractions de molécules en fonction de leur énergie cinétique selon la théorie de Maxwell. Nous remarquons que le pourcentage des molécules caractérisées par une énergie supérieure à une valeur telle que ea augmente lorsque la température augmente. Ainsi, nous avons :

Estimation de facteur stérique, P2
Il n'existe aucune théorie capable de déterminer, a priori, le facteur stérique, P2. En effet, celui-ci ne peut être estimé qu'a posteriori, en comparant les données expérimentales et théoriques correspondant à un système donné. D'ailleurs, son apparition dans les formalismes de la théorie des collisions n'a été faite que pour tenir compte des écarts observés entre les valeurs prédites par la théorie et celles rencontrées expérimentalement.
A titre d'exemple, pour une réaction en phase gazeuse dans les conditions ambiantes, le nombre total de collision, calculé à l'aide de l'équation (3-14) est de l'ordre 1034 s-1.m-3. Si toutes les collisions conduisaient effectivement à une réaction, la vitesse de toute réaction en phase gazeuse serait de l'ordre 1010 mol.m-3.s-1; toutes les réactions seraient pratiquement instantanées.
En pratique, les vitesses de ces réactions sont en moyenne 1010 à 1012 fois plus lentes, ce qui démontre que seule une collision sur 1010 à 1012 est efficace, les autres collisions étant assimilables à des chocs élastiques sans conséquence chimique !
Le tableau suivant présente une comparaison entre les valeurs expérimentalement observées et celle données par la théorie pour quelques réactions en phase gazeuse

Théorie des collisions et la loi de vitesse
En combinant les équations (3-9), (3-11), (3-16) et (3-17), nous pouvons démontrer que la vitesse moléculaire de la réaction s'écrit :
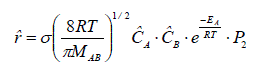
Il est plus commode d'exprimer les différents paramètres de cette équation en terme molaire et non plus moléculaire. Nous obtenons alors :
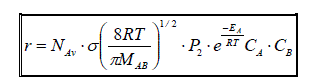
Comparons cette expression à celle obtenue par la combinaison des lois d'Arrhenius et de van't Hoff pour une réaction bimoléculaire élémentaire, à savoir :
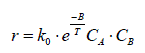
Nous constatons que cette théorie prévoit, conformément à la règle de van't Hoff, que la vitesse de la réaction doit varier avec le produit des concentrations des réactifs. De plus, cette théorie permet de donner une signification physique au facteur pré exponentiel, k0, de la loi empirique d'Arrhenius, appelé facteur de fréquence en le reliant à l'orientation des molécules et à la fréquence de leurs collisions.
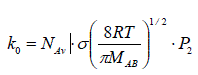
Ce dernier passage n'est pas tout à fait cohérent car k0 dépend de T et n'est pas constante. Toutefois, cette approximation peut être tolérée dans la mesure où, en pratique, dans la plage de variation habituelle de Ea, la variation de la vitesse réactionnelle avec la température est très majoritairement due au terme exponentiel
